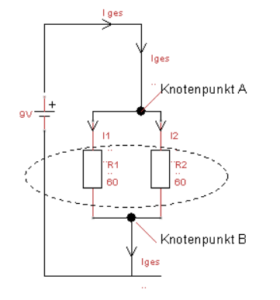
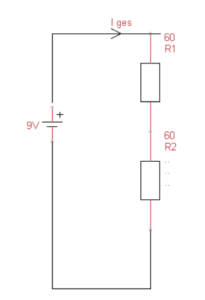
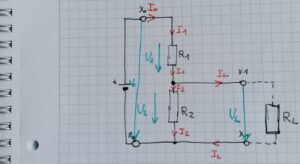
hender – Elektro/ Elektronik-Stammtisch

Widerstand versus Leitwert

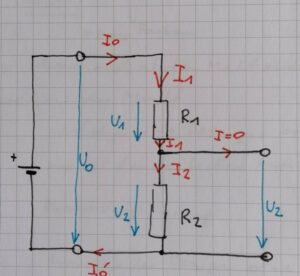
Der elektrische Leitwert hat das Formelzeichen G und wird in Siemens angegeben. Er ist das Reziprok(Kehrwert des el. Widerstandes. G=1/R. daraus ergibt sich: Je kleiner der Widerstand, desto größer ist der Leitwert und umgekehrt. Damit du dir das gut merken kannst gebe ich dir ein Beispiel um es dir zu veranschauliche: Wir haben einen Konzertsaal mit vielen Besuchern. Auf der linken Seite gibt es eine kleine schmale Türe und hinten ein große doppelflügelige Türe. Nun ist das Konzert zu Ende, beide Türen werden geöffnet und alle Zuhörer drängen nach Draußen. Die kleine Türe bieten den Besuchern einen großen Widerstand und leitet nur wenige Personen nach draußen. Während die breite doppelte Flügeltüre hinten für die Zuhörer einen kleinen Widerstand darstellt und viele Personen nach draußen leitet. Daher gilt folgendes.⇒ Je größer der Widerstand, desto kleiner der Leitwert.

kleiner Widerstand, großer Leitwert!
großer Widerstand, kleiner Leitwert!

z.B.

Ein kleiner Widerstand mit 0,02Ω hat einen Leitwert von 5 Siemens.

Ein großer Wiederstand mit 200Ω hat einen Leitwert von 0,05 Siemens.

Ein

Parallelschaltung

Im Gegensatz zur Reihenschaltung ist die Berechnung des Gesamtwiderstandes etwas aufwendiger, aber für dich nicht unlösbar!

Wie du in der obigen Grafik erkennen kannst fließt der Strom Iges von der Batterie zum Knotenpunkt A und teilt sich dortin die zwei Teilströme I1 und I2 auf. Diese fließen dann durch den jeweiligen Widerstand R1 bzw. R2. Nach den beiden beiden Widerständen fließen die beiden „Teilströme im Knotenpunkt B wieder zusammen und bilden wieder den Strom Iges, der zur Batterie zurück fließt. Wir können also sagen Iges=I1+I2.

Und ohne es selbst richtig zu bemerken haben wir das1. Kirchhoffsche Gesetz( Knotenregel) angewendet und auch verstanden. Dieses Gesetz besagt nämlich : Die Summe aller auf einen Knotenpunkt zufließenden Ströme ist gleich groß wie die Summe aller von dem Knotenpunkt abfließenden Ströme. Oder auch anders formuliert: Die Summe aller auf einen Knotenpunkt zu- und abfließenden Ströme ist gleich Null!

Reihenschaltung

Eine Reihenschaltung von ohmschen Widerständen ist recht einfach zu berechnen.

Der gesamte Strom der Batterie Iges fließt (wie in der Grafik oben erkennbar ist) durch den Widerstand R1 und R2 und dann wieder zurück zur Batterie.

Um den Gesamtwiderstand zu berechnen kannst du einfach die Widerstandswerte von R1 und R2 addieren.

Rges=R1+R2 =60Ω+60Ω=120Ω

Rges=120Ω

Nun kannst du mit dem ohmschen Gesetz „I=U/R“ den Strom Iges berechnen.

Iges =U/Rges = 9V/120Ω= 0,075A ⇒ 75mA.

Iges=75mA sprich “ 75 Milliampere“

belasteter Spannungsteiler (Lösung)

Hallo hier nun die Lösung zum Beispiel unbelasteter Spannungsteiler.

Wir beginnen mit folgender Feststellung:

Der belastete Spannungsteiler ist vom Prinzip her gleich wie ein „unbelasteter Spannungsteiler“ mit dem Unterschied dass beim Widerstand R2 parallel ein „Lastwiderstand RL zugeschaltet ist und ein Strom IL zu den Klemmen fließt.
Als erstes berechnen wir den Gesamtwiderstand der Schaltung. Ist dieser ermittelt können wir mit Hilfe vom ohmschen Gesetz den Gesamtstrom Io berechnen, der übrigens gleich groß wie der Strom I1durch den Widerstand R1 ist.(Io=I1).
Mit Jilfe der Formelvom ohmschen Gesetz können wir nun mit dem Strom I1 und dem Widerstand R1 die Spannung U1 berechnen.

belasteter Spannungsteiler (Aufgabe)

Hallo hier habe ich für dich ein weiteres Beispiel das du berechnen kannst. In einer Woche werde ich dir hier eine Lösung dazu anbieten. Bitte warte nicht bis die Lösung kommt! Ich freue mich sehr, wenn du mir schon vorab dein Ergebnis über Kommentarfeld mitteilst. 🙂 Also worauf wartest du? Hol dir Papier und Stift und fange an zu rechnen!

Die Angaben:

Als Spannungsquelle haben wir wieder links eine Batterie mit Uo=12V
R1= 45Ω
R2= 30Ω
RL= 30Ω

Gesucht:

Wie groß ist die Spannung UL an den beiden Klemmen X1?

Die Lösung findest du hier


Continue reading belasteter Spannungsteiler (Aufgabe)

unbelasteter Spannungsteiler (Lösung)

Hallo hier nun die Lösung zum Beispiel unbelasteter Spannungsteiler.

Wir beginnen mit folgender Feststellung:

An den Klemmen von U2 ist nichts angeschlossen.
Der Strom I zu den Klemmen ist Null. I=0
Somit ist der Strom der durch den Widerstand R1 und durch den Widerstand R2 fließt ist gleich groß.
Die WiderständeR1 und R2 sind in <Série geschaltet und können somit addiert werden. (20Ω+60Ω=80Ω)
Die beiden Widerstände liegen an einer Spannungsquelle von 12 V. ⇒ Somit ergibt sich ein Strom 12V/80Ω=150mA
U2 entspricht der Spannung an R2 Wir rechnen also:

U2 =150mA x 60Ω=9V

unbelasteter Spannungsteiler (Aufgabe)

GutenTag! Hier habe ich für dich ein neues Rechenbeispiel. Ein sogenannter „Klassiker“ de in der Elektronik und Elektrotechnik. Der unbelastete Spannungsteiler:

Wir haben folgende Angaben:

Uo: Eine Batterie als Spannungsquelle Uo= 12 V

R1=20Ω

R2=60Ω

Frage: Wie groß ist die Spannung U2 an den beiden Klemmen (rechts im Bild)?

Viel Spaß beim grübeln und rechnen wünscht dir Herbert!

PS: Du hast eine Lösung gefunden, irgendwo hast du einen Knoten drin oder du kommst irgendwie nicht weiter.

⇒ Schreibe mir doch eine Nachricht ins Kommentarfeld. Ich werde dir helfen.

⇒ Es hilft auch mir weiter, wenn du das Kommentarfeld nutzt und mir schreibst wo dich der Schuh drückt.

⇒ So kann ich das Thema meiner nächsten Beiträge besser an deine Bedürfnisse anpassen und genau jene Thema behandeln die dich brennend interessieren.

Wie gewohnt werde ich in einer Woche eine Lösung für dieses Rechenbeispiel posten.

Also dann bis nächste Woche! Schöne Grüße, Herbert.

Klicke hier zur Lösung

Rechenbeispiel1 (Lösung)

Guten Tag lieber Leser! Die Woche ist nun vorbei. Hier nun, wie versprochen, die Lösung zum Rechenbeispiel 1:

Wie du weißt errechnet sich der Strom durch die Formel I=U/R. Du setzt nun die Zahlen aus dem Beispiel ein und erhältst 12 V geteilt durch 40 Ω ⇒

12/40=0,3 A oder anders ausgedrückt 300mA ( 300 Milliampere)

Rechenbeispiel 1

Da du nun das „ohmsche Gesetz kennst, können wir eine erste einfache Berechnung durchführen.

Dazu habe ich für dich ein kleines Beispiel vorbereitet.

Ganz links haben wir eine Batterie mit einer Spannung von 12V (U1). An den Klemmen ist ein Widerstand von 40 Ohm angeschlossen.

Frage: Wie groß ist der Strom (I1) der durch unseren Widerstand (R1) fließt?

In etwa 1 Woche werde ich die Auflösung posten.

Das ohmsche Gesetz:

Die drei Kenngrößen Spannung U, Strom I und Widerstand R stehen in einem proportionalen Verhältnis zu einander. Legst du eine Spannung U und einen konstanten Widerstand R wird sich ein konstanter Stromfluss I durch den Widerstand R ergeben. Verdoppelst du nun die Spannung U wird sich bei gleichbleibendem Widerstand R der Stromfluss I ebenfalls verdoppeln. Wenn du nun den Widerstand R Langsam erhöht wird der Strom I langsam sinken. Die Spannung U die an einem Widerstand R abfällt entspricht dem Produkt von Strom I durch den Widerstand mal dem Wert des Widerstandes R.

U=I*R

Durch umformen dieser Formel kannst du auch I oder R berechnen.

I=U/R oder

R=U/I

In der einschlägigen Literatur findet man das ohmsche Gesetz oft in Form eines Dreieckes dargestellt. Ich finde diese Darstellung sehr gut und habe sie selbst während meines Studiums verwendet. Hinweis: „Du findest sehr einfach heraus wie eine Variable aus den jeweils anderen zwei berechnet erden kann, indem du die gesuchte Variable einfach abdeckst!“

<<<Zum Beispiel: Deckst du U ab, bleibt I*R übrig. ⇒ U=I*R

Deckst du I,ab, bleibt U/R übrig. ⇒ I=U/R

Hier eine Grafik die ich für dich zum einfacheren merken erstellt habe:

( diese Formel verwenden wir vorerst nur für Gleichspannung an einem rein ohmschen Widerständen). Wie es sich mit induktiven oder kapazitiven Blindwiderständen bei Wechselspannungen verschiedenen Frequenzen verhält erkläre ich dir in später folgenden Beiträgen.